はじめに
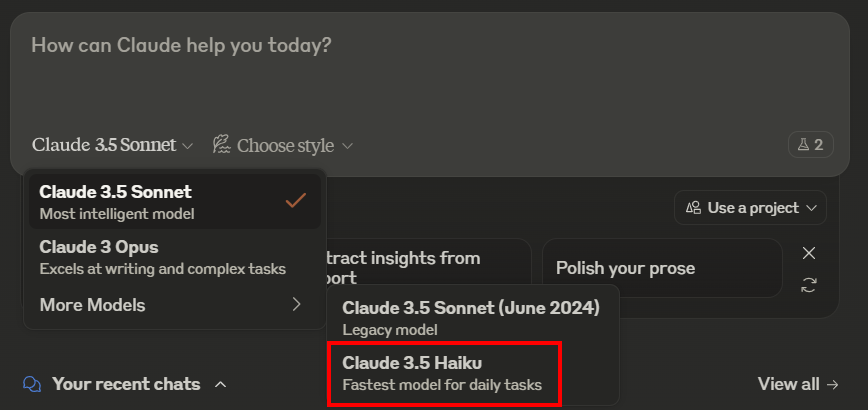
先日、APIの利用が解禁されたClaude 3.5 Haikuですが、ウェブ版とモバイルアプリ版でも利用できるようになりました。
ということで、現行のClaude 3.5 Sonnetとの違いを文章要約とコーディングで簡単に見てみようと思いますので、まだClaudeを触ったことがない方は参考にしてみてください!
英語の文章要約
以下の英語を日本語で要約してください。
Claude 3.5 Haiku, our next-generation fast model, is now available in Claude.ai on the web and in our mobile apps. Claude 3.5 Haiku offers exceptional skills for coding, quick information processing, and short-form content creation. Currently, Claude 3.5 Haiku is available as a text-only model. For tasks requiring image processing, conversations will automatically switch to Claude 3 Haiku.
We have also expanded Claude.ai’s capabilities across file handling and mobile support, including:
Enhanced file support for rich analysis
With the analysis tool toggled on in feature preview, Claude can:
Directly analyze Excel files to pull data, evaluate formulas, recreate a formatted spreadsheet as an Artifact, and more.
Interpret large spreadsheets up to 30MB for instant insights. Track sales, customer behavior, or market trends with fewer data size restrictions.
Improved Claude mobile experience
The analysis tool is now available on our iOS and Android apps, letting you make data-driven decisions wherever you are.
Styles are supported on the iOS app, with Android coming soon, for consistent communication across devices.
以下が要約です:
Claude 3.5 Haikuが、Claude.aiのウェブ版とモバイルアプリで利用可能になりました。このモデルはコーディング、情報処理、短文作成に優れています。現在はテキストのみの対応で、画像処理が必要な場合はClaude 3 Haikuに自動的に切り替わります。
さらに、以下の機能が追加されました:
- 分析ツールを使用することで、Excelファイルの直接分析や30MBまでの大規模スプレッドシートの処理が可能になりました
- iOSとAndroidアプリで分析ツールが利用可能になり、モバイルでのデータ分析が可能に
- iOSアプリでスタイル機能をサポート(Androidは近日対応予定)
以下は、提供された英語テキストの日本語要約です:
Anthropicは、新世代の高速モデルであるClaude 3.5 Haikuを、ウェブサイトとモバイルアプリで利用可能にしました。このモデルは、コーディング、情報処理、短文コンテンツ作成において優れた能力を持っています。現在、テキストのみのモデルであり、画像処理が必要な場合は、自動的にClaude 3 Haikuに切り替わります。
また、Claude.aiのファイル処理とモバイルサポートを拡張し、以下の機能を追加しました:
豊富な分析のための高度なファイルサポート
プレビュー機能のある分析ツールにより、Claudeは以下が可能になりました:
- Excelファイルを直接分析し、データ抽出、数式評価、フォーマットされたスプレッドシートのアーティファクト再作成など
- 最大30MBの大規模スプレッドシートを即座に分析し、売上、顧客行動、市場トレンドを追跡
モバイル版Claudeの機能向上
- iOSとAndroidアプリで分析ツールが利用可能になり、どこからでもデータに基づいた意思決定が可能
- iOSアプリでスタイル機能をサポート(Androidは近日対応予定)
コーディング
Benfordの法則を分析するPythonプログラムを作成してください。なお、同時にダミーデータの生成も行い、分析結果のデモも実施してください。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy import stats
class BenfordAnalyzer:
def __init__(self):
# Benfordの法則による理論的な確率分布
self.benford_dist = {str(d): np.log10(1 + 1/d) for d in range(1, 10)}
def generate_dummy_data(self, size=1000, type='natural'):
"""
分析用のダミーデータを生成する
Parameters:
size (int): データ数
type (str): 'natural' (自然に従うデータ) または 'uniform' (一様分布)
"""
if type == 'natural':
# 指数分布を使用してBenfordの法則に従うようなデータを生成
data = np.exp(np.random.exponential(size=size))
else:
# 一様分布からランダムな数値を生成
data = np.random.uniform(1, 1000, size=size)
return data
def get_first_digits(self, numbers):
"""数値の最初の桁を抽出"""
return [str(n)[0] for n in numbers if str(n)[0].isdigit()]
def analyze_data(self, data):
"""
データを分析しBenfordの法則との適合度を検証
Parameters:
data (array-like): 分析対象の数値データ
Returns:
dict: 分析結果
"""
# 最初の桁を抽出
first_digits = self.get_first_digits(data)
# 実際の分布を計算
digit_counts = pd.Series(first_digits).value_counts().sort_index()
observed_dist = digit_counts / len(first_digits)
# 理論値との比較用にデータを整形
expected_dist = pd.Series(self.benford_dist)
# カイ二乗検定
chi2_stat, p_value = stats.chisquare(
f_obs=digit_counts,
f_exp=[len(first_digits) * self.benford_dist[str(d)] for d in range(1, 10)]
)
return {
'observed': observed_dist,
'expected': expected_dist,
'chi2_stat': chi2_stat,
'p_value': p_value
}
def plot_comparison(self, results, title="Benford's Law Analysis"):
"""分析結果を可視化"""
plt.figure(figsize=(12, 6))
# 観測値と期待値をプロット
width = 0.35
x = np.arange(9)
plt.bar(x - width/2, results['observed'], width, label='Observed', color='skyblue')
plt.bar(x + width/2, results['expected'], width, label='Expected (Benford)', color='lightgreen')
plt.xlabel('First Digit')
plt.ylabel('Frequency')
plt.title(f"{title}\nP-value: {results['p_value']:.4f}")
plt.xticks(x, range(1, 10))
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()
# デモンストレーション
if __name__ == "__main__":
analyzer = BenfordAnalyzer()
# Benfordの法則に従うデータを生成
natural_data = analyzer.generate_dummy_data(size=10000, type='natural')
natural_results = analyzer.analyze_data(natural_data)
analyzer.plot_comparison(natural_results, "Natural Data")
print(f"自然データの分析結果:")
print(f"カイ二乗統計量: {natural_results['chi2_stat']:.2f}")
print(f"P値: {natural_results['p_value']:.4f}")
# 一様分布のデータを生成
uniform_data = analyzer.generate_dummy_data(size=10000, type='uniform')
uniform_results = analyzer.analyze_data(uniform_data)
analyzer.plot_comparison(uniform_results, "Uniform Random Data")
print(f"\n一様分布データの分析結果:")
print(f"カイ二乗統計量: {uniform_results['chi2_stat']:.2f}")
print(f"P値: {uniform_results['p_value']:.4f}")import numpy as np
import matplotlib.pyplot as plt
import math
import random
def generate_benford_data(num_samples=10000, distribution_type='power_law'):
"""
Generate dummy data that follows or deviates from Benford's Law.
Args:
- num_samples (int): Number of data points to generate
- distribution_type (str): Type of data distribution
Returns:
- list: Generated data points
"""
if distribution_type == 'power_law':
# Power law distribution that tends to follow Benford's Law
data = [int(10 ** (np.random.uniform(0, 6))) for _ in range(num_samples)]
elif distribution_type == 'financial':
# Simulated financial data (company revenues, transaction amounts)
base_values = [random.uniform(1000, 1000000) for _ in range(num_samples)]
data = [int(x) for x in base_values]
elif distribution_type == 'uniform':
# Uniform distribution that likely won't follow Benford's Law
data = [random.randint(1, 1000000) for _ in range(num_samples)]
else:
raise ValueError("Invalid distribution type")
return data
def calculate_first_digit_frequency(data):
"""
Calculate the frequency of first digits in the dataset.
Args:
- data (list): Input data points
Returns:
- dict: Frequency of first digits
"""
first_digits = {}
for number in data:
# Skip zero and negative numbers
if number <= 0:
continue
# Extract first digit
first_digit = int(str(abs(number))[0])
first_digits[first_digit] = first_digits.get(first_digit, 0) + 1
# Convert to percentages
total = sum(first_digits.values())
first_digit_percentages = {
digit: (count / total * 100) for digit, count in first_digits.items()
}
return first_digit_percentages
def benford_expected_distribution():
"""
Calculate the expected distribution according to Benford's Law.
Returns:
- dict: Expected percentages for first digits
"""
return {d: math.log10(1 + 1/d) * 100 for d in range(1, 10)}
def chi_square_test(observed, expected):
"""
Perform Chi-square goodness of fit test.
Args:
- observed (dict): Observed first digit frequencies
- expected (dict): Expected first digit frequencies
Returns:
- float: Chi-square statistic
- float: p-value
"""
import scipy.stats as stats
# Prepare data for chi-square test
obs_values = [observed.get(d, 0) for d in range(1, 10)]
exp_values = [expected[d] for d in range(1, 10)]
# Normalize expected values to match total observations
total_obs = sum(obs_values)
exp_values = [total_obs * (v/100) for v in exp_values]
# Perform chi-square test
chi2_stat, p_value = stats.chisquare(obs_values, exp_values)
return chi2_stat, p_value
def visualize_benford_comparison(observed, expected):
"""
Create a bar plot comparing observed and expected distributions.
Args:
- observed (dict): Observed first digit frequencies
- expected (dict): Expected first digit frequencies
"""
plt.figure(figsize=(12, 6))
# Prepare data
digits = list(range(1, 10))
obs_percentages = [observed.get(d, 0) for d in digits]
exp_percentages = [expected[d] for d in digits]
# Create bar plot
bar_width = 0.35
plt.bar([d - bar_width/2 for d in digits], obs_percentages,
width=bar_width, label='Observed', color='blue', alpha=0.7)
plt.bar([d + bar_width/2 for d in digits], exp_percentages,
width=bar_width, label='Expected (Benford\'s Law)', color='red', alpha=0.7)
plt.xlabel('First Digit')
plt.ylabel('Percentage')
plt.title('Comparison of First Digit Distribution')
plt.xticks(digits)
plt.legend()
plt.grid(axis='y', linestyle='--', alpha=0.7)
plt.show()
def analyze_benford_law(data, distribution_type):
"""
Comprehensive analysis of Benford's Law for given data.
Args:
- data (list): Input data points
- distribution_type (str): Type of data distribution
"""
print(f"Benford's Law Analysis for {distribution_type} Distribution")
print("-" * 50)
# Calculate observed first digit frequencies
observed_freq = calculate_first_digit_frequency(data)
# Get expected Benford's Law distribution
expected_freq = benford_expected_distribution()
# Print observed frequencies
print("\nObserved First Digit Frequencies:")
for digit in sorted(observed_freq.keys()):
print(f"Digit {digit}: {observed_freq[digit]:.2f}%")
# Visualize comparison
visualize_benford_comparison(observed_freq, expected_freq)
# Perform Chi-square test
chi2_stat, p_value = chi_square_test(observed_freq, expected_freq)
print("\nChi-square Goodness of Fit Test:")
print(f"Chi-square statistic: {chi2_stat:.4f}")
print(f"p-value: {p_value:.4f}")
# Interpret results
print("\nInterpretation:")
if p_value > 0.05:
print("The data is consistent with Benford's Law (fail to reject the null hypothesis).")
else:
print("The data significantly deviates from Benford's Law (reject the null hypothesis).")
print("\n")
# Main demonstration
def main():
# Test different distributions
distributions = ['power_law', 'financial', 'uniform']
for dist_type in distributions:
# Generate data
data = generate_benford_data(num_samples=100000, distribution_type=dist_type)
# Analyze the data
analyze_benford_law(data, dist_type)
if __name__ == "__main__":
main()おわりに
上記の結果はウェブ版で試したものですが、ウェブ版においては実行速度にそれほど違いは感じませんでした。また、性能的にはやはりSonnetの方が良いように思いますが、APIを通じてそこそこの精度で処理したいという場合にはHaikuの方が使い勝手がよさそうです。価格もSonnetの1/3で済みますしね!

コメント